分析ツールアドインにある「乱数発生」「二項分布」についての実習解説です。
「乱数発生」の「分布」で「二項」を選択した場合の実習例を以下に示します。この例では、成功の確率(p値)が0.5で試行回数が10回の二項分布に従う乱数を100個生成します。これは実質的に公正なコインを10回投げ、そのうちの「成功」(例えば、表が出る)回数をカウントするシミュレーションとみなすことができます。
- 「データ」タブを開き、「データ分析」をクリックします。
- 「データ分析」ダイアログボックスが表示されたら、「乱数発生」を選択し、「OK」をクリックします。
- 「乱数発生」ダイアログボックスが表示されたら、以下のように設定します:
- 「変数の数」: 1 を入力します(乱数列は1つだけ生成します)。
- 「乱数の数」: 100 を入力します(乱数を100個生成します)。
- 「分布」: 「二項」を選択します。
- 「パラメータ」: パラメータ1には0.5(成功の確率p)、パラメータ2には10(試行回数)を入力します。
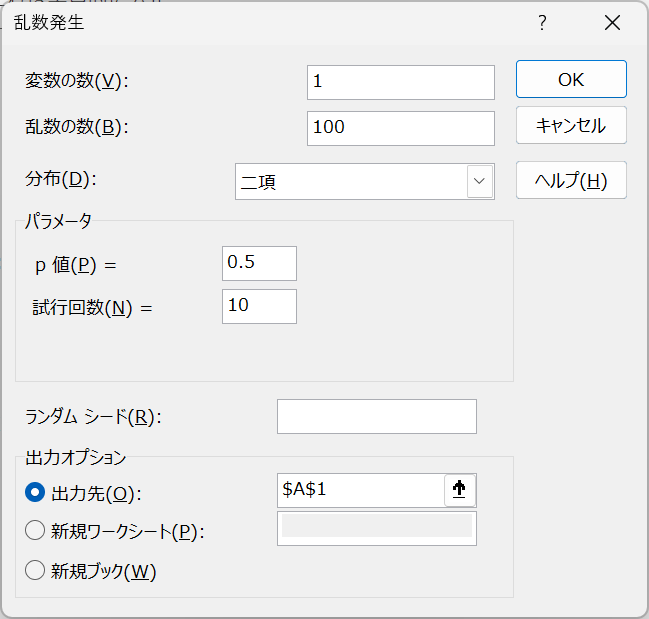
- 「出力範囲」を選択し、例えば A1 セルを指定します。
- 「OK」をクリックします。
これで、A列の1から100までのセルに、成功の確率0.5で試行回数が10回の二項分布に従った乱数が生成されます。生成された各乱数は、公正なコインを10回投げて何回表が出たかを示す数値と解釈できます。
二項分布はベルヌーイ試行(2つの可能な結果を持つ試行)を繰り返す際の成功回数の分布を表します。ここでは、p値(成功の確率)を0.5と試行回数を10と設定したので、各試行で0から10までの成功回数がランダムに生成されます。生成された乱数を確認してみると、大体5回成功することが最も頻繁に起こり、0回や10回成功することはあまり起こらないことを確認できるでしょう。

コメント